m-way search tree
m-way search tree는 최대 m개의 자식을 가지는 tree이다.

- 각 노드는, m~⌊m/2⌋ 개의 children과 m-1~⌊m/2⌋-1 개의 key를 가진다.
- Tip. children의 개수를 기억하면, key의 개수는 -1을 하면 된다.
- 오름차순으로 정렬되어 있다.
B-tree(Balanced tree)
B-tree에서 B는 balance를 의미한다. 여기서 밸런스를 갖춘다는 것은 어느 한쪽으로 치우치지 않고 균형이 맞다는 뜻이다.
B-tree는 m-way search tree + ⍺ 인 tree이다.
다음과 같은 추가 특징들을 갖는다.
- 루트는 최소 2개의 children을 갖는다.
- 모든 external 노드는 같은 레벨(높이)이다. (perfectly balanced)
- 모든 internal 노드는 최소 ⌈m/2⌉ ~ 최대 m 개의 children을 갖는다.
- 여기서, external노드는 leaf 노드를 의미하고, internal 노드는 root와 leaf 노드를 제외한 모든 노드를 의미한다.

m=3일 때, 모든 internal 노드는 2 or 3개의 자식을 가진다. (따라서, 각 노드 별 key의 개수는 1 or 2개이다.)
m=4일 때, 모든 internal 노드는 2,3 or 4개의 자식을 가진다. (따라서, 각 노드 별 key의 개수는 1~3개이다.)
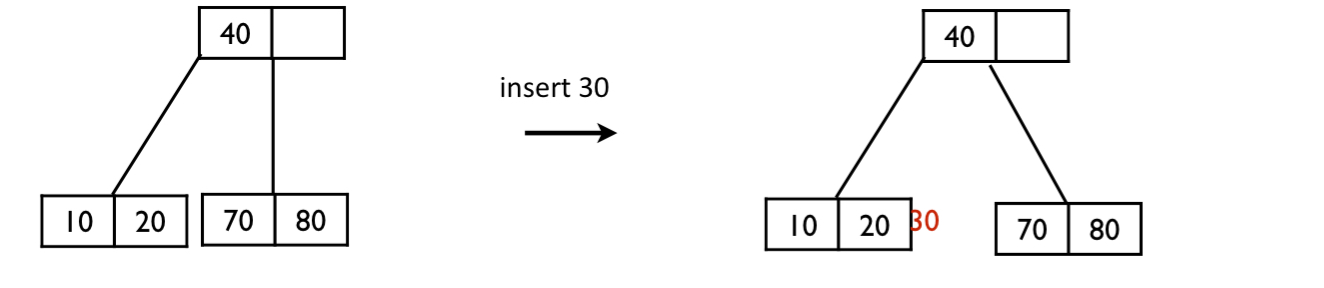
B-tree 연산 - Insertion
1. key rotation
sibling 노드에 공간이 있는 경우 사용 가능한 방법


2. node split
key rotation만으로 해결이 불가능한 경우 사용 가능한 방법
삽입 이후에 overflow가 발생한 경우, 노드를 세 그룹으로 나누어야 한다.
- (a) middle key보다 작은 key들
- (b) middle key
- (c) middle key보다 큰 key들
(b)를 parent로 올리고, (a)와 (c)를 새로운 노드로 만들면 된다.


B-tree 연산 - Deletion
1. key rotation
insertion과 마찬가지로 sibling 노드에 공간이 남아있는 경우 사용 가능한 방법

2. node merging
key rotation만으로 해결이 불가능할 때 사용 가능한 방법
